Atrás
|
TIPOS DE
CÁLCULOS |
TIPOS DE DEDUCCIÓN O REGLAS DE INFERENCIA
La deducción directa
Un argumento es un conjunto de enunciados o proposiciones
entre los cuales una proposición final, llamada conclusión, se sigue
de las otras proposiciones o premisas. Pues bien, llamamos
deducción a un modo de argumentar
tal que el paso de las premisas a la conclusión es necesario.
La deducción formal o lógica consiste en que a partir de
unas premisas, representadas con símbolos, y a través de unas
reglas, obtenemos una conclusión (deducimos la conclusión).
Los símbolos en la lógica de enunciados pueden ser:
Los conectores o juntores: ¬,
&, V, ->, <->
Letras enunciativas: p, q,
r...etc, que representan los enunciados de la argumentación.
Símbolos auxiliares: ( ), I-
(este último signo se utiliza para indicar formalmente la
conclusión):
Ejemplo: "si graniza (g) o nieva (n) entonces, uso paraguas
(p) o no salgo de casa (¬s) . Se da el caso de que graniza (g) . Por
lo tanto, no salgo de casa (¬s) ".
La formalización de este argumento es la siguiente:
( g V n ) -> ( p V ¬s ) , g I- ¬s
Ahora bien; la deducción puede ser directa e indirecta.
Por deducción directa entendemos aquella en la cual, a
través de las premisas, obtenemos la conclusión de un modo directo:
Ejemplo: Si vienes pronto, podremos ir al cine. Has venido
pronto. Conlusión: vamos al cine.
Formalicémoslo: p -> c, p I- c
Ahora bien ¿Cómo se lleva a cabo la deducción formal o
derivación?
El primer paso consiste en escribir las premisas iniciales con
las que contamos, numerándolas y anteponiendo a la numeración un
guión horizontal.
En el segundo paso, aplicando sobre las premisas las reglas de
derivación que luego veremos, numeramos las derivaciones que se
extraigan de ellas, pero en este caso no le antecedemos a los
níumeros que le correspondan ningún guión. El último número
corresponde con la obtención de la conclusión deseada. Veámoslo:
Tomando como ejemplo la formulación anterior, tendremos que
derivar c (la conclusión), de las premisas p -> c y c
-1 p -> c
-2 p
3 c MP 1,2
Las letras que siguen a la línea de derivación tres se
corresponden con las iniciales de la regla de cálculo utilizada, en
este caso, el Modus Ponens: dada una implicación cualquiera,
si se da el antecedente, entonces necesariamente podemos inferir el
consecuente (esto se verá en el próximo capítulo). La numeración que
sigue al nombre de la regla se refiere a las líneas sobre las que se
ha aplicado dicha regla .
Derivemos la siguiente fórmula utilizando el Modus Ponens: p
-> ( q -> r ), p -> q, p I- r
- 1 p -> ( q -> r )
- 2 p -> q
- 3 p
4 q -> r MP 1,3
5 q MP 2,3
6 r MP 4,5
|
La deducción indirecta o reducción al absurdo (
reductio ad absurdum)
En este tipo de deducción obtenemos la
conclusión de modo indirecto, negando la misma conclusión hasta
llegar a una contradicción.
Los pasos de la reducción al absurdo son los
siguientes:
1. Suponemos
hipotéticamente la falsedad de la conclusión:
¬p
2. Esta suposición nos conduce a una
contradicción: ( q & ¬q )
3. Negamos, por lo tanto, la falsedad de la
suposición: ¬ ( ¬p )
4. Afirmamos la
conclusión deseada: p
Antes de realizar un ejemplo concreto sobre la
reducción al absurdo conviene que veamos las reglas en las que
se fundamenta la deducción: las llamadas reglas de inferencia.
|
Modelos
de cálculos
FICHA
EJERCICIOS LÓGICA PROPOSICIONAL
Ejercicio 1º Simple ( Técnica del cabo suelto)
| 1 |
Juan come o ayuna |
1 |
p W q |
P |
| 2 |
No ayuna |
2 |
Ø
q |
P |
| 3 |
Si estudia se siente
satisfecho |
3 |
z
®
r |
P |
| 4 |
Estudia |
4 |
z |
P |
| C |
Luego como y
se siente satisfecho |
C |
p
Ù
r |
C |
| |
|
5 |
p |
REWne
1,2 |
| |
|
6 |
r |
RE®aa
3,4 |
| |
7 |
p
Ù
r |
RIÙ
5,6 que es la C. |
Ejerc. 1º Simple Técnica de red. al
absurdo)
| 1 |
Juan come o ayuna |
1 |
p W q |
P |
| 2 |
No ayuna |
2 |
Ø q
|
P |
| 3 |
Si estudia se siente
satisfecho |
3 |
z
®
r |
P |
| 4 |
Estudia |
4 |
z |
P |
| C |
Luego como y
se siente satisfecho |
C |
p
Ù
r |
C |
| |
|
|
5 |
Ø(pÙ
r) |
Supuesto RRA |
| |
|
|
6 |
ØpVØr |
RM1
5 |
| |
|
7 |
r |
RE®
aa 3,4 |
| |
|
|
8 |
p |
REWne
1,2 |
| |
|
|
9 |
Ør |
REVne
6,8 |
| |
|
|
10 |
rÙØr |
RIÙ
7,9 |
| |
|
|
11 |
Ø(pÙ
r)®(rÙØr) |
RI®
5-11 |
| |
|
12 |
p
Ù
r que es la C. |
RRA 11 |
EJERCICIO 2º SIMPLE ( técnica del supuesto condicional)
| 1 |
Si robas y se entera la policía, te
detienen |
1 |
( p
Ù
q )
®
r |
P |
| 2 |
Tú robas |
2 |
p
|
P |
| C |
Si se entera la policía,
te detienen |
3 |
q
®
r |
C |
| |
|
|
4 |
q |
S ( supuesto) |
| |
|
|
5 |
p
Ù
q |
RIÙ
2,4 |
| |
|
6 |
r |
RE®
aa 1,4 |
| |
|
7 |
q
®
r
que es la C. |
RI®
ms 4-6,
|
Ejercicio 3º Simple (Técnica del supuesto
condicional)
| 1 |
Si Juan viene entonces es verdad que si Nuria se
entera, le manda un
aviso |
1 |
p
®
( q
®
r ) |
P |
| 2 |
Pepita se entera
|
2 |
q |
P |
| C |
Si Juan
viene, Nuria le manda un aviso
|
C |
p
®
r |
C |
| |
|
|
3 |
p |
S |
| |
|
|
4 |
( q
®
r ) |
RE®
1,3 |
| |
|
5 |
r
|
RE®
2,4 |
| |
|
6 |
p
®
r que
es la C. |
RI
®
3- 5 |
Ejercicio 4º Simple ( Método del supuesto)
| 1 |
Si me ha tocado la lotería entonces es verdad que
si
juego tengo suerte
|
1 |
p
®
( q
®
r ) |
P |
| 2 |
He jugado a la lotería
|
2 |
q |
P |
| C |
Si me ha
tocado la lotería, entonces es que tengo suerte.
|
C |
p
®
r |
C |
| |
|
|
3 |
p |
S |
| |
|
|
4 |
( q
®
r ) |
RE®
1,3 |
| |
|
5 |
r |
RE®
4,2 |
| |
|
6 |
p
®
r que es la C |
RI
®
3,5 |
| |
|
|
|
|
Ejercicio 5º Simple ( Técnica o
método del cabo suelto)
| 1 |
Si Juan viene, también viene Ana
|
1 |
p®q |
P |
| 2 |
Nos vamos o salimos corriendo
|
2 |
r V s |
P |
| 3 |
Si
salimos corriendo,Ana no viene
|
3 |
s®Øq
|
P |
| 4 |
No nos
vamos |
4 |
Ør |
P |
| C |
Juan no viene
|
C |
Øp
|
C |
| |
|
5 |
s
|
REV
2,4 |
| |
|
6 |
Øq
|
RE®
aa 3,5
(M.P.)
|
| |
7 |
Øp
que es la C. |
RE®
nc 1,6 (M.T.) |
Ejercicio 5º
Simple (Técnica de reducción al absurdo)
| 1 |
Si Juan viene, también viene Ana
|
1 |
p®q |
P |
| 2 |
Nos vamos o salimos corriendo
|
2 |
r V s
|
P |
| 3 |
Si
salimos corriendo, Ana no viene
|
3 |
s®Øq
|
P |
| 4 |
No nos
vamos |
4 |
Ør |
P |
| C |
Juan no viene
|
C |
Øp
|
C |
| |
|
|
5 |
p
|
SRA |
| |
|
|
6 |
s |
REV 2,4 |
| |
|
|
7 |
Øq
|
RE®
aa 3,5
(M.P.)
|
| |
|
8 |
q |
RE®
aa 1,5 |
| |
|
|
9 |
q
Ù
Øq |
RIÙ
7,8 |
| |
|
|
10 |
p
® (q
Ù
Øq) |
RI®
5-9 |
| |
|
11 |
Øp
que es la C. |
RRA 10 |
PARA HACER MÁS
EJERCICIOS
6º Ejercicio
"SI TE VAN BIEN LOS ESTUDIOS O TIENES MUCHA CAPACIDAD O
DEDICAS MUCHO TIEMPO A ESTUDIAR.
SI TE ANIMAN TUS PADRES TE VAN BIEN LOS ESTUDIOS.
TE ANIMAN TUS PADRES
NO TIENES MUCHA CAPACIDAD
CONCLUSION: LE DEDICAS MUCHO TIEMPO A ESTUDIAR"
1- p
®(r
V n) Si te van bien los estudios o tienes mucha capacidad o dedicas
mucho
tiempo a estudiar
2- m®p
Si te animan tus padres te van bien los estudios
3- m
Te animan tus padres
4-
Ør
No tienes mucha capacidad
CONC: n Le
dedicas mucho tiempo al estudio
1- p
®(r
V n) P
2- m®p
P
3- m
P
4-
Ør
P
5- p
RE®aa(MP)
2,3
6- r V n
RE®aa(M.P.)
5,1
7- n
RE V
4,6 QUE ES LO QUE QUERÍAMOS PROBAR
7º Ejercicio
Yo tengo unos ahorros. Si tengo unos ahorros puedo prestar un poco de
dinero a un amigo. Si no me ayudan mis familiares, entonces
tendré problemas. Luego si no tengo problemas, entonces es que me ayudan mis
familiares y puedo prestar dinero a un amigo.
8º Ejercicio
Si lo considero necesario
compro una caja de diskettes. Si compro la caja de diskettes y no los
pierdo, los uso con los alumnos. Si los uso con los alumnos me puedo
encontrar un virus. Luego, si compro una caja de diskettes puedo encontrar
un virus
9º Ejercicio
"O no aumenta la presión
fiscal o no crece la inversión. Aumenta la presión fiscal. Luego no crece la
inversión"
10º Un caso de
reducción al absurdo
|
1 |
p V q |
|
|
2 |
p
®r
|
|
|
3 |
q
®r
|
|
|
C |
r |
|
|
5 |
|
Ør |
|
6 |
|
Øp |
|
7 |
|
q |
|
8 |
|
r |
|
9 |
|
rLØr |
|
10 |
|
Ør®r
LØr |
|
11 |
r |
|
11º
|
1 |
p
®Ø(qLr) |
|
2 |
p
®
(qLr) |
|
C |
Øp |
12º
13º
14º
|
1 |
(p
V q)
®r |
|
2 |
r®s |
|
C |
(p
V q)
®s |
|
1 - p V q
2 -
Ø q
3 - z
®
r
4 - z
C - p
Ù
r
|
1 - p
®
q
2 - p
z
3 -
Ø
q
4 - z
®
r
5 - s
C - s
Ù
r
|
1
- p
®
q
2
-
Ø
r W q
3
- s
®
Ør
4
- s
5
- s
®
t
C
-
Ø p
Ù
t |
|
1 - p
Ù
q
2 -
p
®
Ør
3 - s
®
r
C
Øs
Ùq |
1 - p V q
2 -
Øq
3 - p
®
z
C z |
1 - p
Ù
q
Ù
r
2 - (p
Ù
q)
®
s
3 -
Øs
C
s
Ù
Øs |
|
1-
p
Ù
q
2- p
®
s
3- s
®Øt
4- q
®t
C t
ÙØt |
1 - p
2 -
p
®
z
3 -
Øs
®
t
C
Øt
®
( s
Ù
z ) |
1-
ØØp
2 -
p
®
q
3 - q
®
z
C z |
EJERCICIOS PRÁCTICOS DE PROFUNDIZACIÓN:
-
¿Alguna de estas reglas es una
regla válida de lógica? (>>>> Formular estos enunciados y aplicar la
comprobación mediante el sistema de tablas de valores).
-
Si una proposición molecular
que consta de dos atómicas relacionadas por conjunción es falsa,
entonces también son falsas las dos atómicas componentes.
-
Si los dos extremos de una
relación de disyunción excluyente implican la falsedad de una misma
proposición, entonces la disyunción inicial es falsa.
-
Si de dos proposiciones sale la
misma implicación, entonces es falsa la oposición excluyente entre
ambas.
-
Si los dos extremos de una
relación de disyunción excluyente implican la verdad de una misma
proposición, entonces es falsa la disyunción inicial.
-
Si vale la contradicción,
entonces todo vale. (O sea si damos por válida una contradicción,
¿de ahí podemos sacar cualquier conclusión?)
-
De una negación se puede sacar
cualquier cosa.
-
Si una proposición incluye la
negación de sí misma, entonces nos lleva a una contradicción y por
tanto, una proposición no puede incluir la negación de sí misma.
-
Si una proposición y su
negación se incluyen mutuamente, eso implica una contradicción.
-
Inventarse alguna posible regla
lógica y comprobar su validez por el sistema de tablas de valores.
EJERCICIOS INTRODUCTORIOS
0º
EJERCICIO SIMPLE
1- ( p
Ù
q ) ®
r
2- p
CONCL
q ®
r
¿de esas dos proposiciones se puede sacar lógicamente esa conclusion
1-(pÙ
q ) ®
r
P(remisa)
2- p
P(remisa)
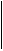 3 - q
S(upuesto)
3 - q
S(upuesto)
4 - p Ù
q
RI
Ù
(2,3)
 5 - r
RE
®aa
(4,1)
5 - r
RE
®aa
(4,1)
6 - q
®
r
RI
®
(3,5) ES LO QUE QUERIAMOS PROBAR
1º
EJERCICIO SIMPLE
1- p
®
( q ®
r ) Si Juan viene entonces es verdad que si Pepita se entera ,
le manda un aviso
2- q
Pepita se entera
CONC:
p ®
r Si Juan viene, Pepita le ha avisado
¿De esas dos proposiciones se puede sacar lógicamente la Conclusión?
1- p
®
( q ®
r ) P
es una premisa
2- q
P
es una premisa
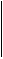 3- p
S supongamos que es
verdad
3- p
S supongamos que es
verdad
4- ( q
®
r ) RE®
1,3
regla elimin condic combinando líneas 1 y 3
5- r
RE®
2,4
regla elimin condic combinando líneas 2 y 4
6- p
®
r RI
®
3,5
introduc condic combinando líneas 3 y 5
2º
EJERCICIO COMPLEJO
1-
r®s
Si estudio apruebo
2- p V
q
Puedo ser premiado o pasar de curso
3-
Ø(Ø
p®s)
No es verdad que si no me premian apruebo
CONCL:
q L
Ør
Puedo pasar de curso y no estudiar
¿vamos a
ver si de esas tres premisas se puede sacar lógicamente esa
conclusión?
1- r®s
P
2- p V
q
P
3-
Ø(Ø
p®s)
P
4-
ØpLØs
Df ®,3
por definición de la condición
5-
Øp
REL
4
6- q
REV
2,5
7-
Øs
REL
4
8-
Ør
RE®
1,7
9- q
L
Ør
RIL
6,8
que es lo que queríamos demostrar
ESQUEMA-RESUMEN: CRITERIOS PARA HACER UN CALCULO LÓGICO ELEMENTAL:
No todos los métodos son aplicables en todos los casos.
SISTEMA DEL SUPUESTO: a partir de un supuesto: vale cuando la conclusión a
demostrar es de tipo condicional
1- p
®
( q ®
r )
Si me ha tocado la lotería entonces es verdad que si
jugaba tendría suerte
2- q
He jugado a la lotería
CONCL:
p ®
r
Si me ha tocado la lotería, entonces tengo suerte.
Como
la conclusión es una condicional, empezamos a razonar suponiendo que se cumpla
la condición
1- p
®
( q ®
r ) P
es una premisa
2- q
P
es una premisa
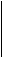 3- p
S
supongamos que es verdad
3- p
S
supongamos que es verdad
4- ( q
®
r ) RE®
1,3
regla elimin condic combinando líneas 1 y 3
5- r
RE®
2,4
regla elimin condic combinando líneas 2 y 4
6- p
®
r
RI
®
3,5
introduc condic combinando líneas 3 y 5
SISTEMA DEL CABO SUELTO DEL QUE TIRAR: a partir de un punto de arranque que se
intuye: se observa atentamente a ver si aplicando alguna de las reglas a alguna
premisa se puede llegar a justificar algo
1. p®q
Si Juan viene, también viene Anita
2. r V
s
Nos vamos o salimos corriendo
3. s®Øq
Si salimos corriendo, Anita no viene
4.
Ør
No nos vamos
 CONC:
Øp
Juan no viene
CONC:
Øp
Juan no viene
1. p®q
P
2. r V
s
P
3. s®Øq
P
4.
Ør
P
5. s
REV 2,4
6.
Øq
RE®
aa 3,5 (M.P.)
7.
Øp
RE®
nc 1,6 (M.T.) LO QUE SE QUERIA DEMOSTRAR
SISTEMA DE REDUCCIÓN AL ABSURDO: si esa proposición fuera verdadera se
llegaría a una contradicción y por tanto no puede ser verdadera, o sea, es
falsa. Para construir el razonamiento negamos la conclusión y vemos que
consecuencias se derivan de esa negación.Si llegamos a ver que se deriva una
contradicción, entonces podemos afirmar que es verdadera esa conclusión.
INTRODUCCIÓN:
REGLA
DE REDUCCIÓN AL ABSURDO.
Si de una proposición
se deriva una contra dicción, esa proposicion es necesariamente falsa
[
p®
(qÙØq)
]
®
Øp
|
p
|
q
|
Øp
|
Øq
|
qÙØq
|
p®
(qÙØq)
|
[
p®
(qÙØq)
]
®
Øp
|
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
Esta
es la base de la demostración de la regla de reducción al absurdo
Analizamos el siguiente caso:
"Si
llevas la contraria a tus profesores (m), entonces no serás bien visto por
ellos(Øn).
Si les
haces la pelota(r), entonces serás bien visto por tus profesores(n)
Por
tanto no es posible llevarles la contraria y a la vez hacerles la pelota.( O
sea, no pretendas a la vez llevarles la contraria y hacerles la pelota porque es
imposible)"
a) por
intuición: ¿qué os parece ese razonamiento? ¿va bien?
b) por
tabla de valores:
[
(m ®Øn)
L
(r
®
n) ]
®
Ø
(m
L
r)
|
m
|
n
|
r
|
Øn
|
m®Øn
|
r®
n
|
m
Lr
|
Ø
(m Lr)
|
(m®Øn)L(r®n)
|
[(m...®Ø(mLr)
|
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
c) por
cálculo: formulación: m
®Øn
r
®
n
Ø
(m
L
r)
Vamos a intentar demostrar esa conclusión por reducción al absurdo
1 - m
®Øn
P
2 - r
®
n
P
3 -
Ø
Ø
(m
L
r) S(=SUPONGAMOS QUE LA CONCL.FUERA FALSA)
4 - m
L
r
REØ
(3)
5 - m
RE
L
(4)
6 -
Øn
RE ®aa
(1,5)
7 - r
RE
L
(4)
8 - n
RE
®aa
(2,7)
9 - nLØn
RIL(6,8)
LO CUALES UNA CONTRADICCION
10 -
Ø
(m
L
r)
REGLA DE REDUCCION AL ABSURDO
EJERCICIOS DE CONFIRMACIÓN
EJERCICIO 1º
UNA
CONVERSACION:
JUAN -
"Yo creo que si te van bien los estudios, entonces esque tú tienes mucha
capacidad o es que le dedicas mucho tiempo a estudiar."
ELLA -
"A mí me parece que si tus padres te animan, entonces los estudios te van bien".
JUAN -
" A MI ME ANIMAN MUCHO MIS PADRES"
ELLA-
" PERDONA, PERO CREO QUE TU NO TIENES MUCHA CAPACIDAD"
JUAN -
"O SEA, QUE PIENSAS QUE LE DEDICO MUCHO TIEMPO AL ESTUDIO"
VAMOS
A EXPRESAR ESTO EN UN LENGUAJE MÁS FORMAL
Y
AHORA EN SIGNOS DE LÓGICA PROPOSICIONAL
{
[
p
®(r
V n)
]
L
(m®p)
L
m
LØr
Ln
}®n
A) POR
INTUICIÓN : hacer un esfuerzo a ver si aparece su coherencia o no
B) POR
TABLA DE VALORES
{
[
p
®(r
V n)
]
L
(m®p)
L
m
LØr
Ln
}®n
C) POR
CALCULO PROPOSICIONAL
1- p
®(r
V n) Si te van bien los estudios o tienes mucha capacidad o dedicas mucho
tiempo a estudiar
2- m®p
Si te animan tus padres te van bien los estudios
3- m
Te animan tus padres
4-
Ør
No tienes mucha capacidad
CONC:
n Le dedicas mucho tiempo al estudio
1- p
®(r
V n) P
2- m®p
P
3- m
P
4-
Ør
P
5- p
RE®aa(MP)
2,3
6- r V
n RE®aa(M.P.)
5,1
7- n
RE V
4,6 QUE ES LO QUE QUERÍAMOS PROBAR











