FILOSOFIA  D E    L A    C I E N C I A    

          ALGUNOS PROBLEMAS ACTUALES

  I N T R O D U C C I O N   

         Este tema es amplísimo. No tenemos más remedio que sintetizarlo y esto según un cierto criterio de ordenación, que en nuestro caso será el siguiente: 

• la matemática como sistema formal axiomático

• la matematización de lo real y sus límites  

• la verdad en la matemática y en las ciencias de la naturaleza  

• física y filosofía  

• inducción y probabilidad  

• naturaleza de las leyes y teorías científicas  

         Por su amplitud  trataremos independientemente los temas 3º y 6º.  Parece razonable que, dada la amplitud del tema, seremos especialmente sintéticos.  

TEMA 1º LA MATEMATICA COMO SISTEMA FORMAL AXIOMATICO 

  ▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀

Introducción:

  la metateoría

  la metamatemática como raíz del enfoque especial de este tema  

1º)  L A   M A T E M A T I C A 

DEFINICIÓN CLÁSICA = "ciencia que estudia el número y la extensión" (trasnochada)

           SUI GENERIS = "lo que aparece en los libros de Matemáticas" ( parecida a la definición de Física que dió Bridgman, Nóbel de Física).

           ORGANIGRAMA 

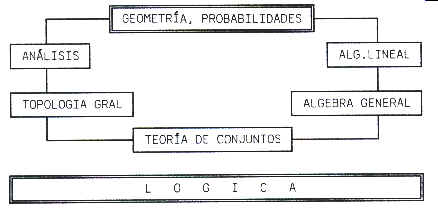  Nota: el fundamentar la matemática en la teoría de conjuntos y en la lógica  es  la  base de la revolución de las matemáticas modernas. Se llegó a esto buscando una mayor coherencia y consistencia. En esta línea han aportado especialmente Hilbert, Cantor y Russell.

  2º  APLICACION A LAS MATEMATICAS DE LOS CRITERIOS DE UN SISTEMA FORMAL AXIOMATICO       

a) AXIOMATIZACION DE LAS MATEMÁTICAS SEGÚN EUCLIDES  

    Si Aristóteles axiomatizó parte de la Lógica, Euclides fue el primero que aplicó la axiomatización a una rama de las matemáticas, en su obra "Elementos" de Geometría del círculo y de la recta, y de la teoría de los números.  

AXIOMAS ("dignidades") proposiciones de base, evidentes (no necesitan demostración).

POSTULADOS ("supuestos")   proposiciones de base, no evidentes ni demostrables (ej:por un punto exterior a una recta sólo se puede trazar una paralela).

TEOREMAS   proposiciones no evidentes, pero demostrables a partir de los axiomas, de los postulados o de otros teoremas (no son, pues, de base).

b) AXIOMATIZACION DE LAS MATEMÁTICAS EN LA ACTUALIDAD  

a)) líneas generales:  

  ‑ a los axiomas de tipo euclideo se les llama "axiomas materiales"

  ‑ hoy se prefieren "axiomas formales" = proposiciones sobre cuya verdad o no verdad no se hace cuestión, sino que se establecen como fundamento de todas las demás proposiciones del sistema axiomático formal. Se trata de algo formalizado que si está bien basado es fecundo y si no, se autodestruye.  

b)) no existe un solo sistema para todas las matemáticas  

  ‑ la lógica de clases utiliza el de Huntington, o los de Birkkoff y Maclane

  ‑ la teoría de conjuntos los de Nemann‑Bernays‑Gödell

  ‑ la aritmética, el sistema de Peano

  ‑ la geometría euclidiana, el de Hilbert

  ‑ etc.  

c)) un ejemplo: la aritmética axiomatizada según Peano  

1- NOCIONES  PRIMITIVAS      

• CERO ---------------------------------------------- 0  

• NUMERO ----------------------------------------- N  

• SUCESOR --- ' (se adosará a un número, de forma que x' = sucesor de x)  

2 - AXIOMAS  

   3º)  LOS LIMITES DE ESTAS FORMALIZACIONES

a) los requisitos de todo sistema formal axiomático

•   consistencia y no contradicción

•   complexión, completud o completitud

•   decidibilidad

•   independencia

b) los límites propios de la lógica que sirva de base a la axiomatización:

•   la decidibilidad sólo se da en el cálculo de predicados monádicos, pero no en el de predicados poliádicos (demostrado por CHURCH en 1936)

• la lógica de conjuntos (lógica cuantificacional superior) no puede ser presentada como sistema completo (demostrado por Gödel en 1931)

• diversidad de "cálculos": para un solo asunto hay muchas formas de expresarlo en cálculo  

c) los límites propios de ciertas ramas de la matemática

    En 1931 Gödell afirma que "en todo sistema axiomático formal lo suficientemente rico para contener la aritmética usual, existen proposiciones indecidibles desde el interior del sistema".

    Para decidirlas habría que salir del sistema y crear un metasistema y así al infinito.  

EJEMPLOS:  

1º teorema de FERMAT

    "es imposible resolver la ecuación  equis elevado a la n, más y elevado a la n es igual a z elevado a la n, cuando n es > 2 "

    No se ha conseguido una demostración general, aunque los mejores matemáticos lo han conseguido para 3, 5 y 7  

2º la conjetura de GOLDBACH

    "parece que cualquier número par puede expresarse como la suma de dos números primos  " Ejemplo 2 = 1+1; 4 = 3 + 1; 6 = 5 + 1; 8 = 5 + 3; 10 = 7 + 3; etc

  ¿ ES ESTO VALIDO PARA TODO NUMERO PAR ?

    A pesar de reiterados esfuerzos nadie ha encontrado respuesta a esta cuestión en ningún sistema axiomático aritmético.  

TEMA 2º LA MATEMATIZACION DE LO REAL Y SUS LIMITES  

  ▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀

      Nos fijamos ahora en otro aspecto de la matemática. Ya no atendemos a sus aspectos formales sino a su relación con la realidad, a la que de alguna forma pretende referirse. Es claramente un aspecto complementario del anterior.

1ª PARTE: BREVE HISTORIA DE LA MATEMATIZACION DE LA NATURALEZA                                 │

TRES PASOS  

•   siglo XV ‑‑‑> revolución astronómica

•    siglo XVII ‑‑‑> revolución física

•   siglo XVIII ‑‑‑> revolución química     

     LÍNEA COMÚN  

• 1  buscaban un CONOCIMIENTO ESTABLE, RIGUROSO, OBJETIVO ... DE LA NATURALEZA  

• 2  y lo van consiguiendo por el camino de la CANTIDAD

  • . las RELACIONES CUANTITATIVAS se pueden conocer exactamente  

  • . las RELACIONES CUALITATIVAS sólo en cuanto se pueden reducir a cuantitativas. Por ejemplo: la temperatura se puede apreciar objetivamente por la dilatación mensurable del mercurio  

  • . no se trata ya de conocer "esencias"  

          el mejor medio para llegar a la certeza científica consistía en "REDUCIR" el objeto de sus investigaciones a este aspecto cuantitativo al ser fecundo este método, cobra gran prestigio y sus cultivadores tienen la tentación de convertir sus conclusiones en metafísica

CONSECUENCIAS de esta matematizacion de la naturaleza  

• valoración del fenómeno (lo que aparece) como objeto de la ciencia  

• nuevo concepto de causalidad  

  •   antes: CAUSA = ser que influye realmente en el ser de otro  

  •   ahora: CAUSALIDAD = vínculo existente entre varios fenómenos de un modo constante, expresable matemáticamente  

• visión más global de toda la realidad con ayuda del instrumento matemático  

ESQUEMAS DE MATEMATIZACION DE LA NATURALEZA

(A) ESQUEMA  M E C A N I C I S T A  

núcleo = LA NATURALEZA ES UNA ENORME MAQUINA: todo lo que sucede en la naturaleza se explica por una serie de piezas (figura y extensión) moviéndose (movimiento)  

justificación  

• se empezó a aplicar la matemática al estudio de la mecánica  

• en este campo triunfó y se tendió a usar el prototipo de la mecanización como paradigma de toda la naturaleza  

•  la fantasía ayudaba mucho a "crear" esas máquinas y a hacer inteligible y cercana la naturaleza  

•   Según esto, se cree que toda la naturaleza debe explicarse por modelos mecánicos. Ejemplo: Renato Descartes.

(B) ESQUEMA  D I N A M I C I S T A  

núcleo = LA NATURALEZA HAY QUE ENTENDERLA COMO UN GRAN CAMPO DE FUERZAS EN JUEGO  

justificación

    en su esfuerzo por matematizar la realidad, Descartes dejó fuera nociones tan importantes como la de fuerza NEWTON

  - un sistema matemático del mundo centrado sobre la fuerza de gravedad

  - el concepto de campo de fuerza será muy fecundo después:

           gravitatorio ═══> electromagnético ═══> nuclear

  - muy equilibrado  

•  un sistema matemático del mundo a través de mónadas (átomos - fuerza)

•  escaso éxito por haberlo mezclado con metafísica y con teología

  (C) ESQUEMA  A T O M I S T A  

núcleo = LA NATURALEZA ESTA COMPUESTA DE PARTÍCULAS INDIVISIBLES

sentido = se sitúa a otro nivel que los dos esquemas anteriores inicialmente fue compatible con ellos luego, al convertirse en conquista de la realidad, superó los caducos esquemas mecanicistas y dinamicistas  

justificación

  a) como enfoque filosófico: se apoya en Demócrito y en seguidores posteriores  

  b) como teoría científica

  antecedentes: los 4 elementos de Aristóteles, los tres de Paracelso (S,Hg,ClNa), "flogisto" de Stahl

   estudio de las propiedades físicas de los gases:

     ‑ los gases compuestos de partículas moviéndose

     ‑ análisis cuantitativo: se descubren una serie de leyes

       . al reaccionar, su peso no varia (Lavoisier)

       . se combinan según relaciones ponderables invariables (Proust)

       . se combinan según proporciones múltiples (Dalton)

       . relaciones volumétricas (Gay‑Lussac)

  ‑ tabla periódica de Mendeleiev

  ‑ se aplicó esta teoría a la cristalografía y a toda la física

  ‑ hoy se admite, más ampliada y profundizada

  ‑ esta historia podría seguir hasta nuestros días

2ª PARTE: LINEAS PARA VALORAR ESTE PROCESO   Y SU APLICACION HOY                

LO MAS POSITIVO

•  exactitud y rigor demostrativo

•  fecundidad: dan pie a nuevas investigaciones; tienen innumerables aplicaciones técnicas.  

SU LIMITACION MAS SERIA

    prescinde de aspectos fundamentales de la realidad (DEJA DE LADO TODO LO QUE NO SE PUEDE REDUCIR A EXPRESION MATEMATICA).  

PELIGROS

•   reduccionismo ( creer que lo que no se pueda reducir a matematica es falso, inexistente o inútil y entonces se "reduce" mucho la realidad )  

• extrapolación : saltar del terreno científico empírico a otros terrenos que no lo son

ALGUNAS OBSERVACIONES PARA CADA UNO DE LOS ESQUEMAS DE MATEMATIZACION  

al  m e c a n i c i s m o:  

• existe el peligro de saltar a mecanicismo filosófico

• en los seres orgánicos resulta una visión empobrecedora

• no consigue explicar ni la luz ni la estructura intraatómica  

• su gran mérito es haber vulgarizado que la naturaleza material se puede ver bien a través de unas gafas matemáticas    

al  d i n a m i c i s m o  

•  ha sido un gran mérito el introducir el fecundísimo concepto de fuerza  

• ¿cómo podría Leibniz formar algo extenso a partir de elementos‑fuerza‑inextensos?  

• enuncia el cómo de la gravitación,pero,en modo alguno, el por qué  

al  a t o m i s m o  

• teoría confirmada con una serie de descubrimientos del siglo XX  

• no simple esquema mental fecundo sino "realidad"  

• en sentido físico, no filosófico  

ALGUNAS CUESTIONES PENDIENTES PARA PROFUNDIZAR

•  la matematización de la geometría y su dificultad para conectar con la realidad ( tres geometrías opuestas)

•  la gran dificultad de matematizar los elementos de las ciencias humanas  

• la estadística: una matematización muy limitada y su discutible generalización  

TEMA 3º FISICA Y FILOSOFIA 

▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀  

                            Es importante no olvidar la clave epistemológica en que  nos situamos.  

(1) LA CRISIS DE LA FISICA

    (Cfr.tema "La verdad en las matemáticas y la verdad en las ciencias de la Naturaleza" apartado 4º de la segunda parte)  

(2) LA CRISIS DE LA METAFISICA

    entendemos por metafísica un

         A ) "conocimiento científico

         B ) sobre la realidad en cuanto tal"  

    La puesta en duda de sus propios fundamentos por el positivismo ha llevado al neopositivismo: al acentuar el rasgo A se niega la posibilidad del rasgo B; la defensa de un contenido vital por parte del existencialismo y el vitalismo ha llevado a descuidar su fundamento: se acentúa el rasgo B y se pierde el rasgo A.  

    Durante el siglo XX la metafísica no ha sido capaz de clarificar las bases y los principios universales de las ciencias. La crisis de la metafísica es responsable de que perdure la crisis de la física.  

(3)  POSTURA DE LOS FISICOS  

a) intrusista :

        desacreditar a la metafisica por teórica o por no justificable y "sacar conclusiones metafísicas" de sus estudios físicos.

        Ejemplo: doble lectura: principio de indeterminismo y principio de inderterminación  

b) pragmatista : 

        la física se justificaría por sus resultados prácticos la cuestión de la verdad puede quedar en suspenso, como objeto de mera e inútil "especulación metafísica". Lo positivo, lo indudable es que la física es útil, obtiene resultados tangibles y cambia las formas de vida. Subyace una identificación de verdad con utilidad  

c) formalista :

        se busca el fundamento de la física no fuera sino dentro de la ciencia misma; se cultivan las ciencias formales que sirven para formalizar y hacer avanzar la física: la matemática y la lógica.  

(4) LINEAS PARA UNA POSTURA SUPERADORA DE LA CRISIS  

A) "concepto histórico de verdad"  

  ‑ caer en la cuenta de que todo lo humano es histórico

  ‑ superar la creencia tradicional de que el conocimiento no puede ser a la vez histórico y verdadero

  ‑ adoptar la doble dimensión: diacrónica y sincrónica teniendo en cuenta que

    ‑ el concepto de verdad no es unívoco

    ‑ el cuerpo de la física no es homogéneo

  ‑ historia significa "creatividad"

B) "clarificar las tareas de la física y de la metafísica"  

    hace falta una filosofía de las ciencias que no sea ninguna de las ciencias concretas sino que estudie sus fundamentos. He aquí algunas posibles líneas de reflexión:  

la    f  í  s  i  c  a

    no es meramente empírica, es también metempírica / se refiere a parte de lo real, aunque fijándose en aspectos generales / recorta su objeto aplicando ciertos conceptos‑base: masa, espacio, fuerza / se verifica retornando a su propio campo / hace discursos metempíricos / se refiere a la totalidad de la experiencia  

la    m e t a f i s i c a

    se refiere a la totalidad

    hace discursos metafísicos (no metempíricos)

    estudia el sentido del todo, la relación de las cosas con la totalidad, afronta las cosas por las que el hombre se juega la vida.

TEMA 4º LA INDUCCION Y LA PROBABILIDAD 

▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀

(1) INDUCCION  

* concepto elemental lógico aristotélico

   ‑ el salto lógico de lo universal a lo particular (ejemplo:  si todos tienen una cualidad, entonces algunos la tienen)  se llama DEDUCCION

  ‑  el salto lógico de lo particular a lo universal (ejemplo:  si algunos roban, todos roban) se conoce como INDUCCION

* diversos conceptos de inducción  

A) induccion MATEMATICA o impropia(según algunos). Si F vale para "n" y si vale para "n+1", entonces F vale para cualquier número. Confronta con los axiomas de Peano.

B) inducción SUMATIVA o inducción completa(según otros). Si 1, 2, 3, 4 y 5 son todos los elementos de la clase "a" y si F conviene a 1, a 2, a 3, a 4 y a 5, entonces F conviene a todos los elementos de la clase "a".

C) inducción ABSTRACTIVA o proceso mediante el cual se abstraen conceptos a partir de la multiplicidad de experiencias

D) inducción PROPIA

   ‑ procedimiento conclusivo: de unos enunciados ---> otros  enunciados

   ‑ procedimiento amplificativo: de algunos particulares se   salta a lo general

   tipos de inducción propia:

    a) primaria: de hipótesis simples llega a leyes (induc. de primer orden)                        secundaria: de hipótesis  complejas llega  a teorías (induc. de 2º orden )

    b) inclusivas: acumula sumatoriamente datos(UNO A UNO)

       exclusivas: excluye hipótesis que incluyen muchos casos posibles (POR GRUPOS)  

  LA INDUCCION CIENTIFICA QUIERE SER PROPIA Y EXCLUSIVA

Nota: para profundizar en el concepto de inducción a lo largo de la historia confronta los temas de historia especialmente el que plantea el punto de vista de Bacón y de Galileo.

      Por razones de brevedad no repetimos todo lo que vamos a exponer con detalle en el tema siguiente en torno a la estructura esencial del método inductivo.

(2) PROBABILIDAD  

* concepto elemental: "algo que puede suceder" (son más las  posibilidades para el sí que para el no)

* conceptos técnicos: