La Prueba por Casos
La Prueba por Casos es
la regla básica que permite eliminar el conjuntor en dos enunciados
de un argumento. El esquema de esta regla de inferencia sería el siguiente:
Esta regla afirma que si tenemos
una disyunción A
B
y en una línea
de una derivación introducimos un supuesto A (primer miembro de la disyunción)
del que derivamos la conclusión
C en otra línea, y además introducimos otro supuesto, B (segundo miembro
de la disyunción original) del que también derivamos C en otra línea, entonces
estamos legitimados para deducir C como conclusión de todo ello.
Veamos cómo funciona esta regla con un ejemplo.
Ejemplo de uso de la Prueba por Casos
Prueba el siguiente argumento:
| Vemos que hay que conseguir el enunciado s,
que es el consecuente de las dos implicaciones de las líneas 2 y 3.
También observamos que los dos antecedentes de las medionadas implicaciones
son los dos miembros de la disyunción de la línea 1. Pues bien, comenzaremos
abriendo un supuesto q, y despés otro supuesto r. Si a partir de cada uno
de estos dos supuestos conseguiemos deducir s,
entonces los cancelaremos y habremos conseguido la solución. Empezamos suponiedo
q: |
|
| A continuación vemos que podemos
aplicar el Modus
Ponens a las líneas 2 y 4 para conseguir s,
con lo cual cancelamos el supuesto abierto la línea anterior: |
 |
1. |
qr |
|
|
2. |
q s |
|
|
3. |
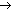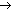rs |
 s |
 |
4. |
q |
|
 |
5. |
s |
MP 2,4 |
|
| Ahora abrimos un nuevo supuesto con r,
con idea de conseguir también s y cancelarlo: |
|
1. |
qr |
|
|
2. |
qs |
|
|
3. |
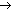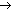rs |
s |
 |
4. |
q |
|
 |
5. |
s |
MP 2,4 |
|
6. |
r |
|
|
| Y aplicando el Modus
Ponens entre las líneas 3 y 6, ya podemos cancelar este segundo
supuesto con el objetivo cumplido: conseguir s a partir de r: |
|
1. |
qr |
|
|
2. |
qs |
|
|
3. |
rs |
s |
|
4. |
q |
|
|
5. |
s |
MP 2,4 |
|
6. |
r |
|
|
7. |
s |
MP 3,6 |
|
| Finalmente, ya podemos aplicar la Prueba
por Casos a la disyunción de la línea 1 y los supuestos abiertos
entre
las líneas 4 y 5 y 6 y 7, por lo que escribimos el enunciado s en la línea
8 y damos por terminada la prueba: |
|
1. |
qr |
|
|
2. |
qs |
|
|
3. |
rs |
s |
|
4. |
q |
|
|
5. |
s |
MP 2,4 |
|
6. |
r |
|
|
7. |
s |
MP 3,6 |
|
| Finalmente, ya podemos aplicar la Prueba
por Casos a la disyunción de la línea 1 y los supuestos
abiertos entre las líneas 4 y 5 y 6 y 7, por lo que escribimos
el enunciado s en la línea 8 y damos por terminada la prueba: |
|
1. |
qr |
|
|
2. |
qs |
|
|
3. |
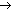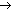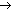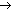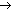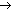rs |
s |
|
4. |
q |
|
|
5. |
s |
MP 2,4 |
|
6. |
r |
|
|
7. |
s |
MP 3,6 |
| |
8. |
s |
Cas 1,4-5,6-7 |
|
Fíjate en esto...
En la justificación de la línea 8 hemos
escrito la abreviatura de la Prueba por Casos: Cas,
seguido de la expresión 1,4-5, 6-7; con
ello aludimos
a las líneas involucradas en la Prueba
por Casos: la ínea 1,
donde está la disyunción de la que partimos, las líneas 4 a 5, que son las
del primer supuesto subsidiario, y finalmente las líneas 6 a 7, las del segundo
supuesto.
Es el momento de practicar lo aprendido sobre el La
prueba por casos en
la siguiente página.
Página siguiente
